Cost Function

The first important step to apply linear regression is to define the cost function.
Cost function will tell us how well/how fit the model is doing.
We should look for more suitable w and b values based on the result.
We are going to want to find values of w and b that make the cost function small.
Our aim is to get minimum cost.

m : number of training example
y : output variable in the training set
y^ : prediction
y – y^ ==> error
(y- y^)² ==> squared error
Squared error cost function is by far the most commonly used one for linear regression.

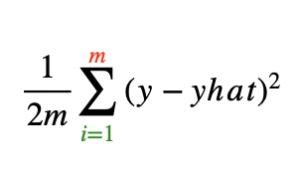
import numpy as np
import matplotlib.pyplot as plt

x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480,  430,   630, 730,])

#try to find optimal values. it will minimize cost.
w = 210
b = 2

def compute_cost(x_train, y_train, w, b):
    m = x_train.shape[0]
    prediction = np.zeros(m)
    cost =0
    #model f(x) = wx + b
    for i in range(m):
        prediction[i] = w*x_train[i] + b
        cost += (prediction[i] - y_train[i])**2
    averageCost = cost / (2*m)
    return averageCost, prediction

cost, prediction = compute_cost(x_train,y_train,w,b)

print(cost)
plt.plot(x_train, prediction, c="b", label = "Our Prediction")
plt.scatter(x_train, y_train, c="r", marker="x", label = "Actual Values")
plt.title("House Pricing")
plt.xlabel("Size")
plt.ylabel("Price")
plt.legend()
plt.show()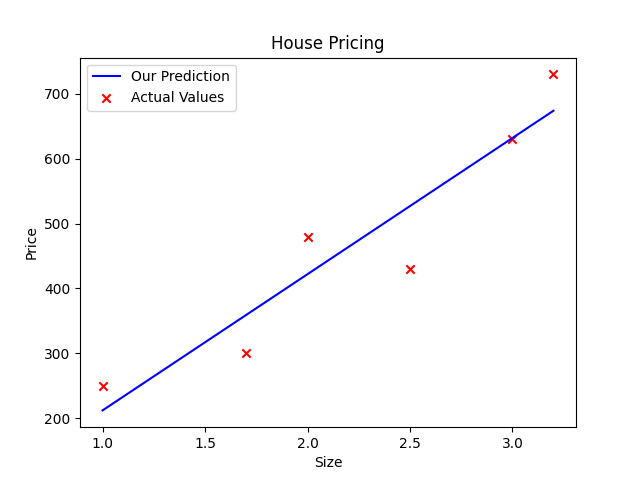

How the cost function can be used to find the best parameters for your model?
Gradient Descent Algorithm is used to automatically find the values of parameters w and b that give you the best fit line. It aims to minimize the cost function J.

For linear regression with the Squared Error cost function, you always end up with a bowl shape.

Gradient Descent helps you go down hill.

• look around, choose direction to take a baby step
• take a tiny baby step
• until you find yourself at the bottom of this valley (at local minimum)