The algorithm can run into a problem called overfitting. Overfitting can cause the algorithm to perform poorly.
To solve this problem:
Regularization will help you minimize the overfitting and get the algorithms to work much better.
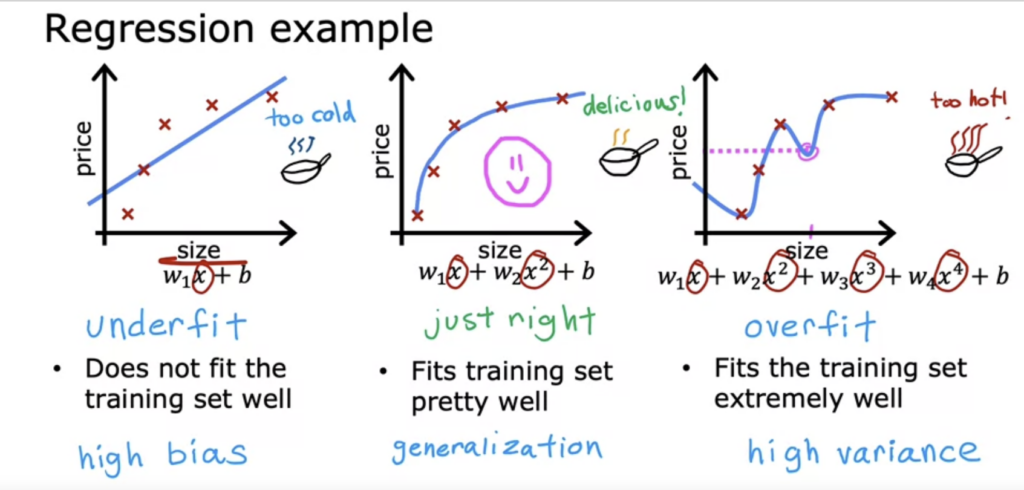
What is overfitting? fits the training set extremely well. The algorithm is trying to fit every single training example. NOT GOOD MODEL. It has high variance. It does not look like the model will generalize to new examples. If your training set were just even a little bit different, then the function that the algorithm fits could end up being totally different. Despite doing very well on the training set, does not look like it will generate well to new new examples. If you have too many features, then the model may fit the training set well, but almost too well or overfit and have high variance. If you have too few features, it underfits and has high bias.
- two different machine learning engineers
- two different test test
totally different predictions or highly variable predictions => the algorithm has high variance
Generalization : you want your algorithm to do well, even on examples that are not on the training set. That is called “Generalization”. It means to make good predictions even on brand new examples that is has never seen before.
Here lets say there are two features :
- Fit the data with degree = 1; Note ‘underfitting’.
- Fit the data with degree = 6; Note ‘overfitting’
- tune degree to get the ‘best fit’
- add data:
- extreme examples can increase overfitting (assuming they are outliers).
- nominal examples can reduce overfitting
Addressing Overfitting : debugging and diagnosing things that can go wrong with learning algorithms
to address overfitting:
1-collect more training data
2-fewer features (select features to include or exclude) selected features : the best set of features: feature selection ( disadvantage : loss information)
all features + insufficient data ==> overfit
3-) regularization: reduce the size of parameters W[j]
f(x) = 13x – 0.23x^2 + 0.000014x^3 – 0.00001x^4 + 10 here 0.000014 and 0.00001 are small values
Regularization lets you keep all of your features, but they just prevents the features from having an overly large effect which sometimes can cause overfitting.
Continue to Cost Function with Regularization