Three Ingredients of Machine Learning
• MODEL (The final product)
A piece of code with some parameters that need to be optimized
• ERROR FUNCTION (Performance Criterion )
The function that you use to judge how well you set the parameter values
• LEARNING ALGORITHM (Training)
The algorithm that optimizes the model parameters using the error function.
to determine an accurate model through optimizing an objective function.
In machine learning, the corresponding objective function is often referred to as a loss or cost function
• Optimization is a procedure of adjusting the parameters of the model in order to minimize the cost function by using one of the optimization techniques.
Linear Regression
• The most commonly used loss function for regression is the Least Squared Error
Logistic Regression
• Logistic regression calculates the class membership probability for
one of the two categories in the dataset
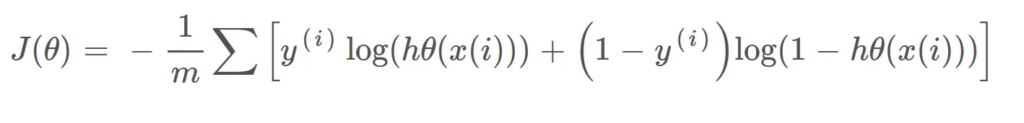
Okey, how do we reduce the cost value. Well, this can be done by using Gradient Descent. The main goal of Gradient descent is to minimize the cost value. i.e. min J(θ).
Derivative of a function f is the rate of change of the function’s output wrt input variable.
- A partial derivative is the derivative with respect to one variable of a multi-variable function.
- The gradient is then the collection of these partial derivatives.
We find optimal value by computing the first derivative f(x) of the function f(x) with respect to x and setting it to 0:
All points for which the first derivative is zero are referred to as critical points of the optimization problem.
• A critical point might be a maximum, minimum, or saddle point (such a point is neither a maximum nor a minimum.)
• How does one distinguish between the different cases for critical points?
The second derivative (i.e., derivative of the derivative) will be positive for minima.
A univariate function f(x) is a minimum value at x = xo with respect to its immediate locality if it satisfies both f'(xo) = 0 and f(xo) > 0.
Bivariate Optimization : In this case, one can compute the partial derivatives of the objective function. This principle is generalized with the use of the Hessian matrix. Instead of a scalar second derivative, we have a matrix of second- derivatives,

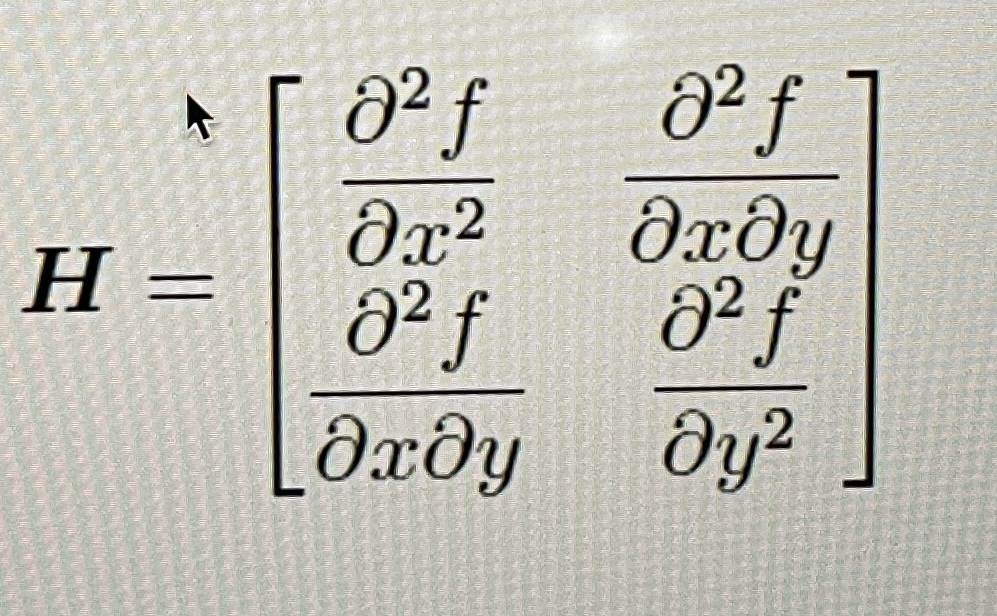
Multivariate Optimization is like Bivariate Optimization