Which parameters to include or which ones to include? It may be hard. You may not know which are the most important features and which ones to penalize. So, the way regularization is implemented to penalize all of the features, you penalize all wj parameters. shrink all of them by adding the regularization term.
The regularization term is added to the Cost function. The regularization term is like the following formula.
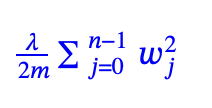
You have to choose a number for lambda.
minimize the cost function : to fit training data well by minimizing the cost function
minimize the regularization cost: try to minimize keep wj small
if lambda 0 : overfits : no regularization
if lambda 10^10 : underfits : it try to minimize the reg. cost, so to minimize regularization term, the algorithm will choose w1, w2, w3 extremely close to 0, then f function will be equal b.
choose lambda how to balance(trade off) between cost function and regularization cost
balance : minimizing cost function and keep wj parameters small
Including this term encourages gradient descent to minimize the size of the parameters w1, w2, w3…
Simpler model
less likely to overfit
to work much better
reg_cost = 0
if lambda_ != 0:
for j in range(n):
reg_cost += (w[j] ** 2)
reg_cost = (lambda_ / (2 * m)) * reg_cost
Gradient descent with regularization:
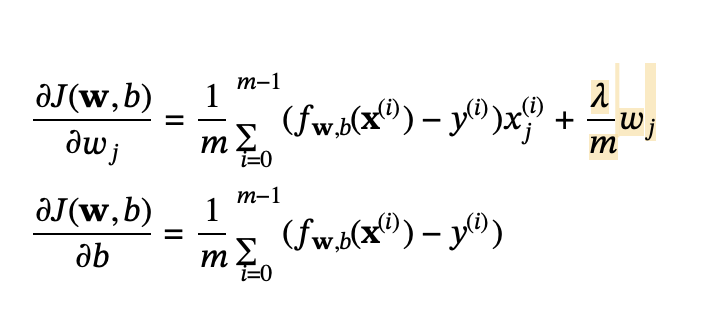
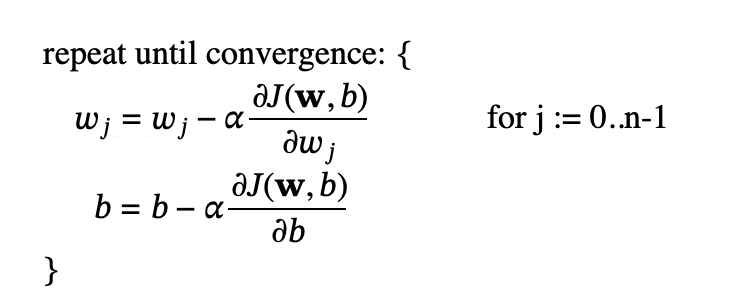
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(z):
g = 1 / (1 + np.exp(-z))
return g
def compute_cost_linear_reg(X, y, w, b, lambda_=1):
m = X.shape[0]
n = len(w)
cost = 0.
for i in range(m):
f_wb_i = np.dot(X[i], w) + b
cost = cost + (f_wb_i - y[i]) ** 2
cost = cost / (2 * m)
reg_cost = 0
for j in range(n):
reg_cost += (w[j] ** 2)
reg_cost = (lambda_ / (2 * m)) * reg_cost
total_cost = cost + reg_cost
return total_cost
np.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
def compute_cost_logistic_reg(X, y, w, b, lambda_=1):
m, n = X.shape
cost = 0.
for i in range(m):
z_i = np.dot(X[i], w) + b
f_wb_i = sigmoid(z_i)
cost += -y[i] * np.log(f_wb_i) - (1 - y[i]) * np.log(1 - f_wb_i) # scalar
cost = cost / m
reg_cost = 0
for j in range(n):
reg_cost += (w[j] ** 2)
reg_cost = (lambda_ / (2 * m)) * reg_cost
total_cost = cost + reg_cost
return total_cost
np.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
def compute_gradient_linear_reg(X, y, w, b, lambda_):
m, n = X.shape
dj_dw = np.zeros((n,))
dj_db = 0.
for i in range(m):
err = (np.dot(X[i], w) + b) - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + err * X[i, j]
dj_db = dj_db + err
dj_dw = dj_dw / m
dj_db = dj_db / m
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_ / m) * w[j]
return dj_db, dj_dw
np.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 1
dj_db_tmp, dj_dw_tmp = compute_gradient_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )
def compute_gradient_logistic_reg(X, y, w, b, lambda_):
m, n = X.shape
dj_dw = np.zeros((n,))
dj_db = 0.0
for i in range(m):
f_wb_i = sigmoid(np.dot(X[i], w) + b)
err_i = f_wb_i - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + err_i * X[i, j]
dj_db = dj_db + err_i
dj_dw = dj_dw / m
dj_db = dj_db / m
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_ / m) * w[j]
return dj_db, dj_dw
np.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.9
dj_db_tmp, dj_dw_tmp = compute_gradient_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )
X_train = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
y_train = np.array([0, 0, 0, 1, 1, 1])
import copy, math
def gradient_descent(X, y, w_in, b_in, alpha, num_iters, lambda_):
J_history = []
w = copy.deepcopy(w_in) # avoid modifying global w within function
b = b_in
for i in range(num_iters):
# Calculate the gradient and update the parameters
dj_db, dj_dw = compute_gradient_logistic_reg(X, y, w, b, lambda_)
# Update Parameters using w, b, alpha and gradient
w = w - alpha * dj_dw
b = b - alpha * dj_db
# Save cost J at each iteration
if i < 100000: # prevent resource exhaustion
J_history.append(compute_cost_logistic_reg(X, y, w, b))
# Print cost every at intervals 10 times or as many iterations if < 10
if i % math.ceil(num_iters / 10) == 0:
print(f"Iteration {i:4d}: Cost {J_history[-1]} ")
return w, b, J_history # return final w,b and J history for graphing
w_tmp = np.zeros_like(X_train[0])
b_tmp = 0.
alph = 0.1
iters = 10000
w_out, b_out, _ = gradient_descent(X_train, y_train, w_tmp, b_tmp, alph, iters, lambda_tmp)
print(f"\nupdated parameters: w:{w_out}, b:{b_out}")