Vectorization

Why vectorization?

• to handle multiple input features
• to make your code shorter
• to make linear regression much faster, much more powerful

Vector Dot Product

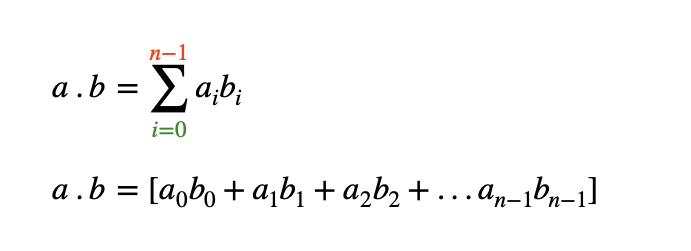
The dot product multiplies the values in two vectors element-wise and then sums the result. Vector dot product requires the dimensions of the two vectors to be the same.

dot product a.w = aT@w = np.matmul(aT,w) matmul = matrix multiplication calculation

import numpy as np

def my_dot(a,b):
    result =0
    for i in range(a.shape[0]):
        result += a[i]*b[i]
    return result
print(a,b)

import time
tic = time.time()
print(my_dot(a,b))
toc = time.time()
print(f"Loop version duration: {1000*(toc-tic):.4f} ms ")
tic = time.time()
print(np.dot(a,b))
toc = time.time()
print(f"Vectorized version duration: {1000*(toc-tic):.4f} ms ")

Loop version duration: 0.0162 ms
one. step at a one time, one step after another
Vectorized version duration: 0.0150 ms
So, vectorization provides a speed up in this example.NumPy dot function uses parallel hardware in your computer. It allows efficient computation. This is critical in Machine Learning where the data sets are often very large. The computer can get all values of the vectors w and x, and in a single step, it multiplies each pair of w and x with each other all at the same time in parallel.

Now, Multiple Variable Linear Regression with Vectorization…